How to Fold a Spaceship
Turning an origami hobby into a career designing deployable spacecraft

Folding origami in space; that certainly was not on my bucket list in middle school as I was spiraling into my newfound paper-folding passion. All I wanted to fold was dragons. Even when a friend’s father sent me a video of a self-assembling, origami-inspired, walking robot, I considered the ancient Japanese art to be a hobby separate from my career aspirations. Then, five years later in college, I discovered the publication corresponding to that very same video was central to my freshman research fellowship. I knew I had found my field. As an engineer, I utilize the same creative problem-solving and visual-spatial skills that were useful to me in my artistic hobbies.
I was very lucky to come across a field that so perfectly fit my interests — as well as incredible mentors who supported me along the way — and I hope to pay it forward. If you stick around to read this article, I will:
Give you an introduction to the mathematics behind origami,
Describe why it is useful in space applications,
Discuss how I happened across this (very niche) field that turned my hobby into an exciting and gratifying career path.
Hold up, did you say space origami?
As we push deeper into space, we need large structures. Larger antennas tens of meters in diameter for communication. Larger solar panels as we get further from the sun. New propulsion methods such as solar sails. Telescopes need huge lenses and better imaging requires sunshields and starshades to block out unnecessary starlight. What do all of these space structures have in common? They do not fit in a rocket.
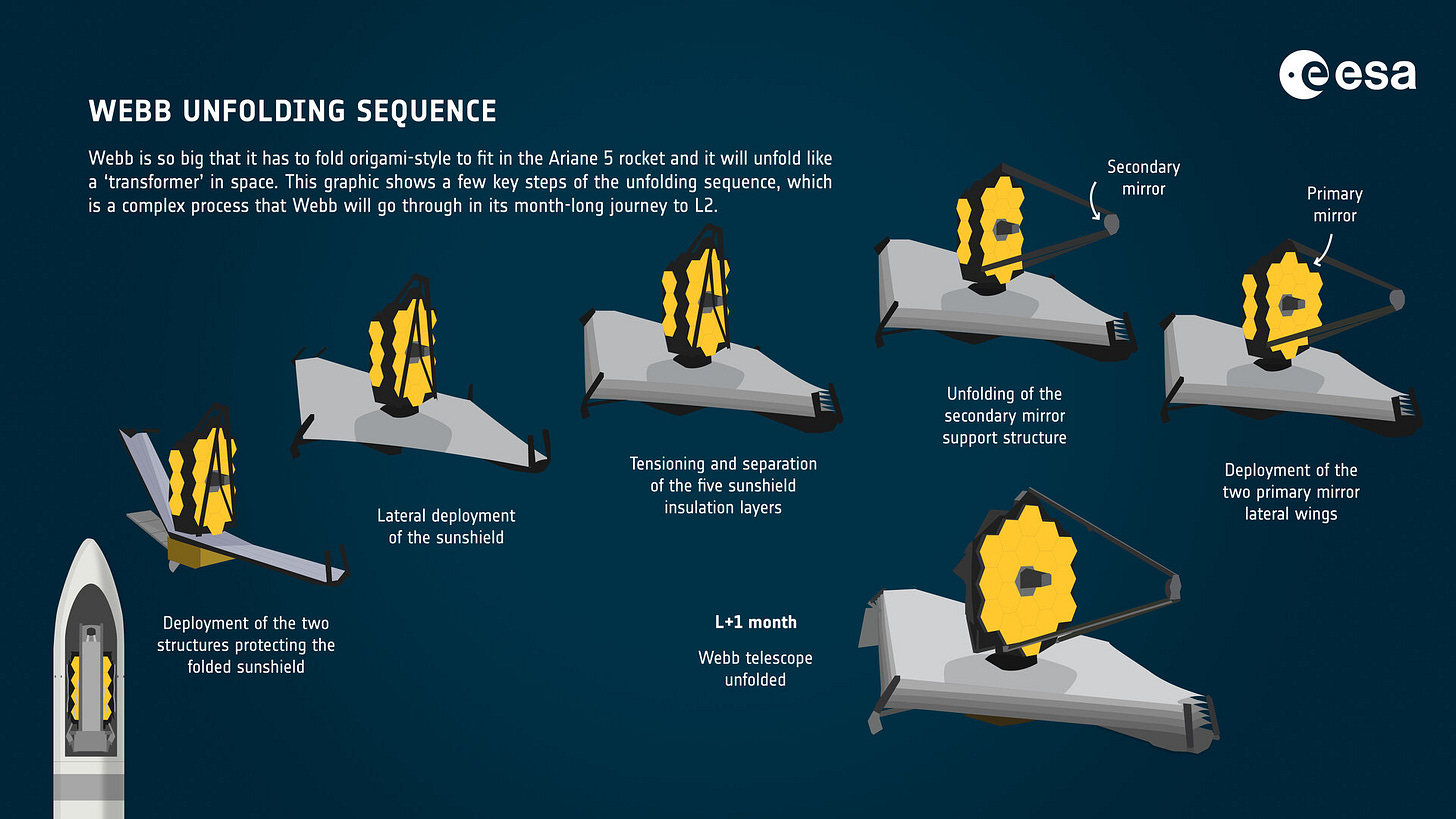
The sunshield of the James Webb Space Telescope measures 21.2 by 14.2 meters (think basketball court, or standard swimming pool). The largest commercial rocket fairings top out at around 5.4 meters in diameter (not much bigger than your bedroom). We’d need major technological breakthroughs for that number to get any bigger.
Enter the field of deployable structures — or, as it’s more fun to call it — space origami! All of these structures need to be carefully folded up in order to fit into a rocket. Then, once in space, they need to be able to unfold without direct human help. This unfolding has to be predictable (so we can model all the potential failures beforehand and either avoid them or know how to fix them) and reliable (so the structure assumes the correct shape once deployed and does not damage itself). Spacecraft are expensive, so there’s a lot riding on correct deployment. For decades, engineers have been turning to the ancient Japanese art of origami for answers.
Let’s take a step back: The basics of complex origami
Origami may be considered an art form, but much like Newton’s laws in physics, it relies on strict mathematical rules. Once you understand these rules, the rest is practice and following the patterns. Let’s start with a simple (and maybe familiar) example: the paper crane.
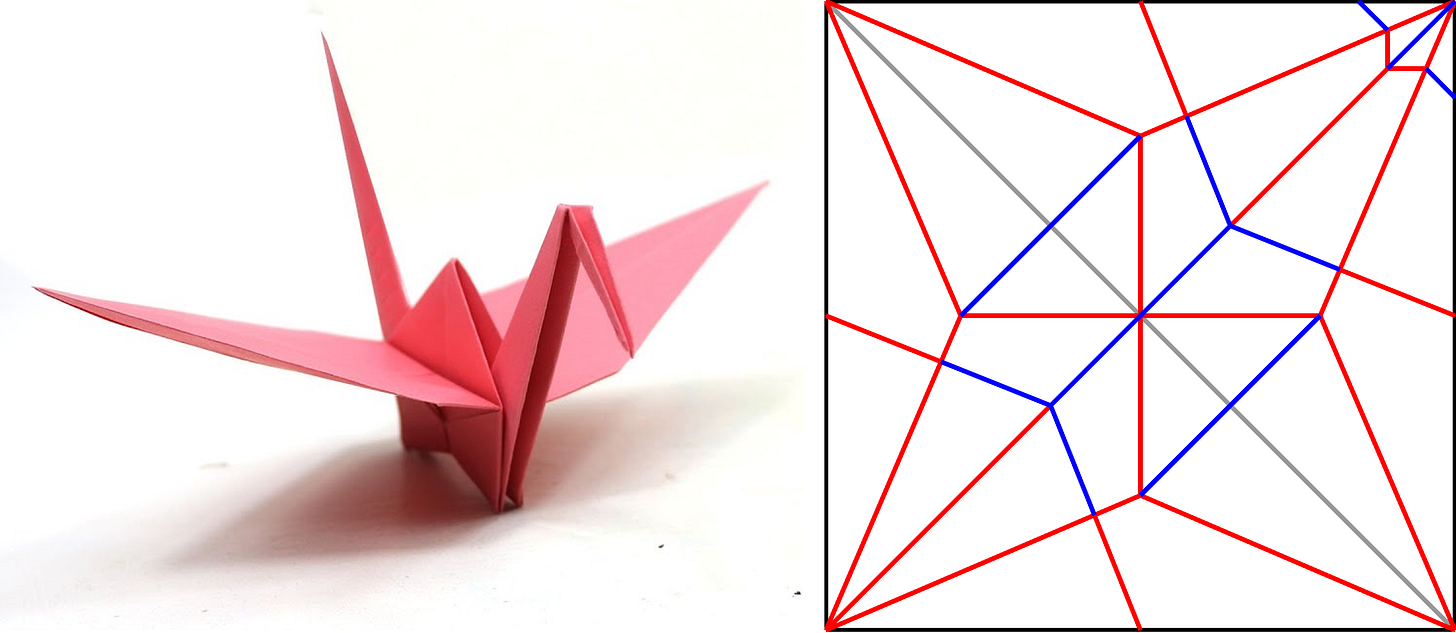
On the left is the paper crane as you know it. On the right is what we call a crease pattern. This is the blueprint that shows all the necessary folds to produce the crane. The red lines are mountain folds (that “come out” of the paper), and the blue lines are valley folds (going “into” the paper). As you can guess, a crease pattern is not a full set of instructions: it does not tell you the order in which to make the folds, and what references you may need. It shows only the folds in the completed model. In fact, some crease patterns don’t even specify mountain vs. valley assignments.
Folding a model from a crease pattern is sort of like a riddle, and that’s the fun of it! See if you can figure out what’s what in the photo above. I’ll give you some hints: the head has the smallest features, so it’s probably the densest part of the crease pattern. Long pointy parts like wings and tails tend to end up at the corners of the square. Think about the symmetry in the completed model.
Now that you’ve familiarized yourself with the crane crease pattern, back to the math. The great origami physicist Robert Lang breaks it down into four rules as follows:
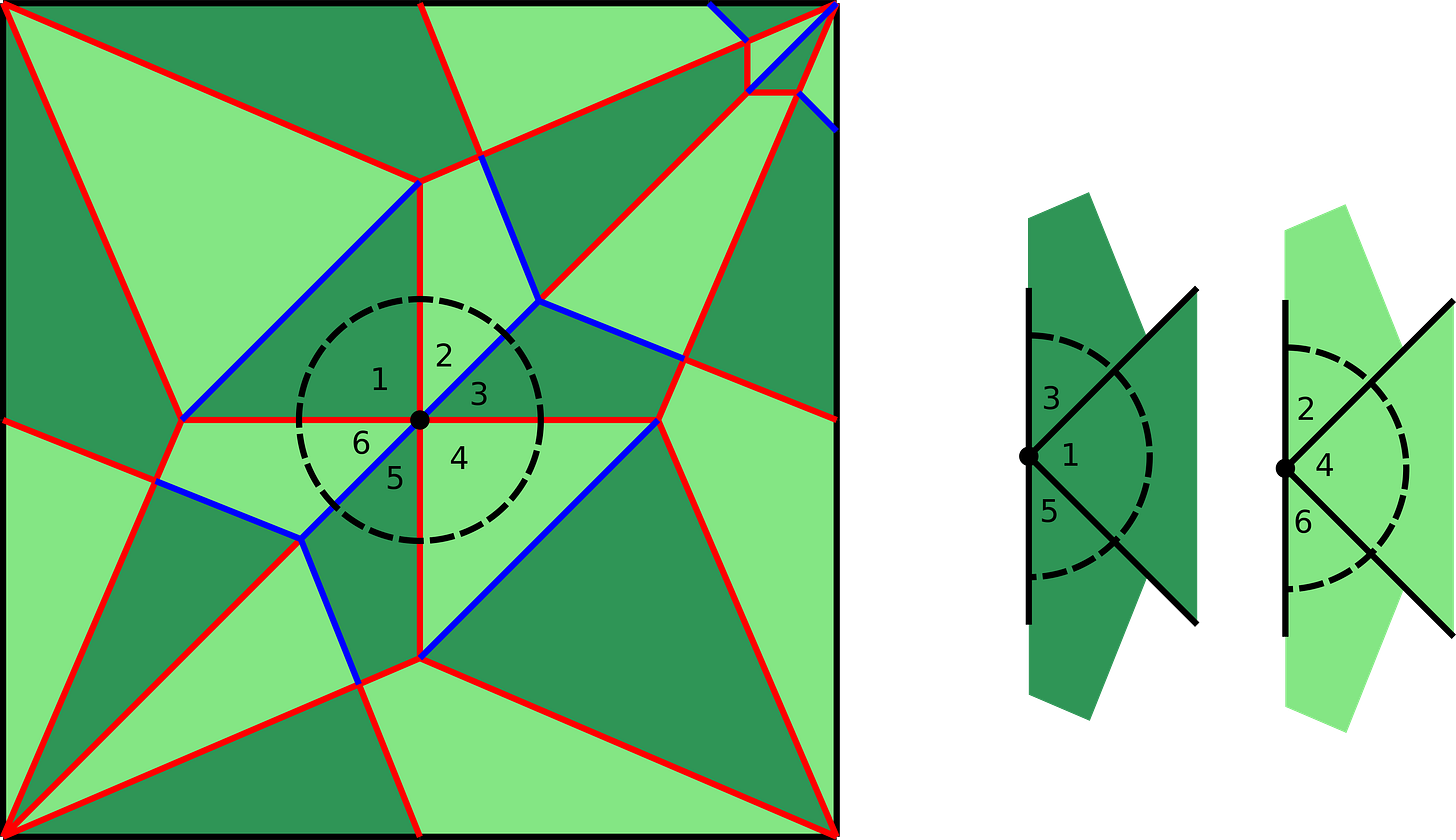
Maekawa’s Theorem: An even number of crease lines meet at every vertex, and at every vertex, the difference between the number of valley folds and number of mountain folds is always two. You can confirm this at every vertex on the crane crease pattern.
Two-colorability: Every crease pattern, no matter how complex, can be colored with only two colors such that no two adjacent panels have the same color.
Kawasaki’s Theorem: If you sum the degree of every second “wedge” around each vertex, they add up to 180°. This ensures that the paper will fold flat at every vertex.
No Self-Penetration: In the folded form, the layers cannot intersect one another.
All origami design principles follow from these rules, and from here the crease pattern design process can be abstracted enough that a computer algorithm can do it for anything you may possibly want to fold (though I won’t get into that here). Robert Lang covers these rules and more in his fantastic TED talk:
Now let’s crank it up a notch. One of my all-time favorite models to fold is Satoshi Kamiya’s Ancient Dragon. The crease pattern and completed model are shown below. You get teeth, toes, horns, wings, and more all from one square sheet of paper, no cuts.

How would you go about folding this? Looks intimidating, right? But look in the top left corner. Does that green square look familiar? That’s right, it’s the crane! And now we know how to fold a crane. It’s no different here, there’s just more paper attached. The rest of the crease pattern can be similarly broken down into smaller approachable chunks. Once you build up experience folding simpler models from crease patterns, you begin to notice the same patterns embedded in more complicated models.

If you’re interested in playing around with crease patterns but don’t want to deal with messy paper, check out the online Origami Simulator.
The simulator can fold origami in real-time, and they have a huge variety of example crease patterns to play around with. You can even upload your own!
Bending the rules for spacecraft
So what do dragons have to do with folding spacecraft? For the large part, the four central rules of origami apply in the exact same way. In fact, unlike complex origami where intricate details are common, for spacecraft folding designs, simplicity is usually key. The more complex the crease pattern, the more points of potential failure. But there are some key exceptions to the rules. I will explore some of these exceptions through a project I contributed to as an intern at JPL: Starshade.
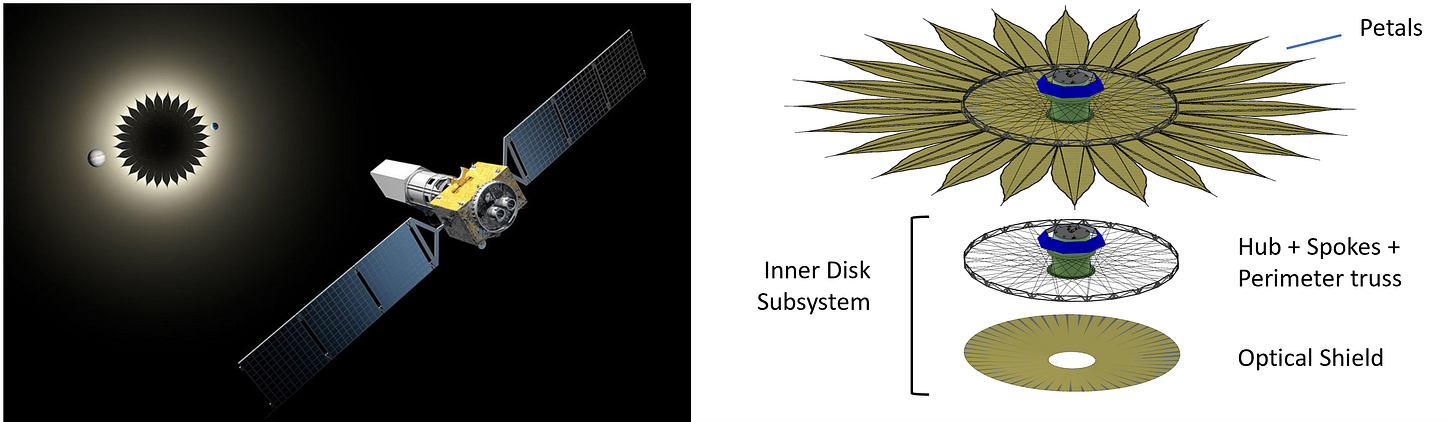
Starshade is a concept for an external occulter to a telescope that would block the light of a distant star such that the telescope can image exoplanets orbiting around the star. Neglecting a lot of details, it would be like you holding your hand up to block the sun so you can see your surroundings better. Except the shape of your hand was specially engineered to cause the destructive interference of diffracting light waves, and you are thousands of kilometers from your hand.
Starshades have a sunflower-like shape (the optics of which I won’t get into) with outer petals and an inner disk supporting them. In order to effectively block starlight, starshades must be tens of meters in diameter, deploy with sub-millimeter level shape-accuracy, and be completely opaque once deployed. This makes for a tricky folding problem.
You can learn more about Starshade and see how it unfolds in this video:
When folded, the entire structure is wrapped around a central hub (containing the actual spacecraft bits - propulsion, communications, etc). Let’s look at the optical shield that blankets the inner disk to block out light. Its unfolding process looks something like this:

And the flat version of its crease pattern looks like this:
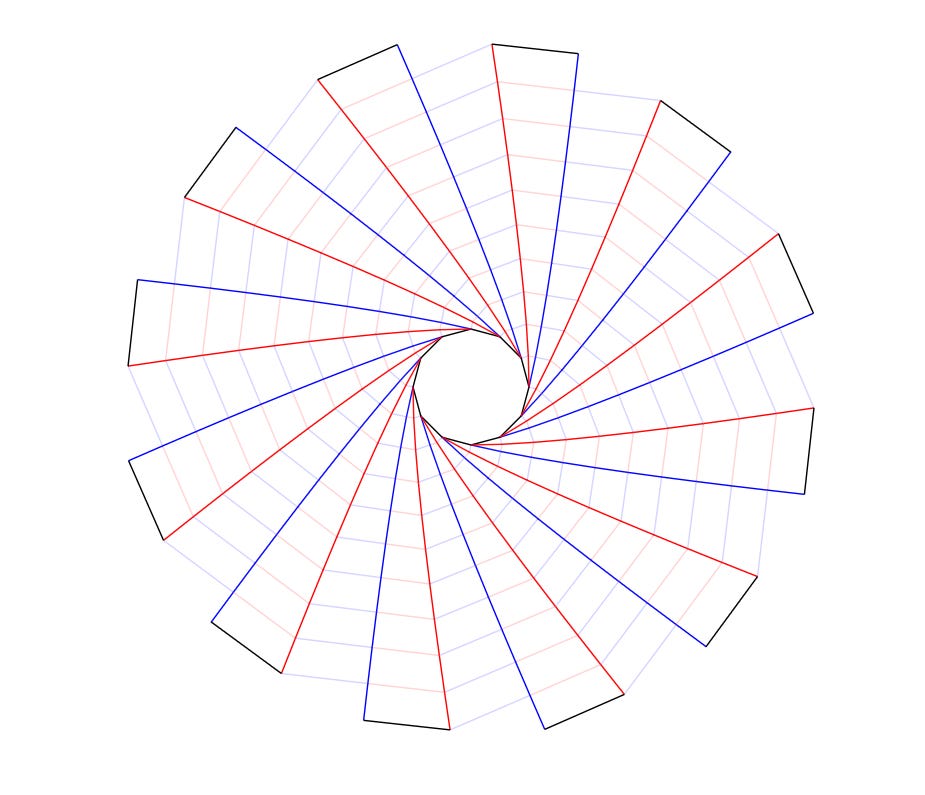
Let’s walk through the rules. Maekawa’s theorem and two-colorability hold (you can check the former at any vertex). Kawasaki’s theorem not quite. You see, the optical shield is not flat — it is actually a very shallow cone. This means the the total angle around some vertices is slightly less than 360°, so the sum of alternating angles can no longer be exactly 180°. This is called an angular defect, and it becomes even more apparent when folding doubly-curved or irregular surfaces (like parabolic reflector antennas for example). In fact, origami in engineering can be categorized into two groups: developable (can be folded from a flat sheet of material) and non-developable (often trickier to manufacture because it’s not from a flat sheet).
We also run into a problem with self-penetration. The rules of origami assume that the paper is of negligible thickness. In order to fold origami neatly, you use very thin paper for this reason. Most origami-inspired structures, however, have some very non-negligible thickness. If you don’t account for this, the material will “run into” itself when folding and keep the structure from folding completely. There are many methods of dealing this problem, often called thickness accommodation methods. For Starshade, thin slices of material were strategically removed around each vertex to allow for smooth folding.
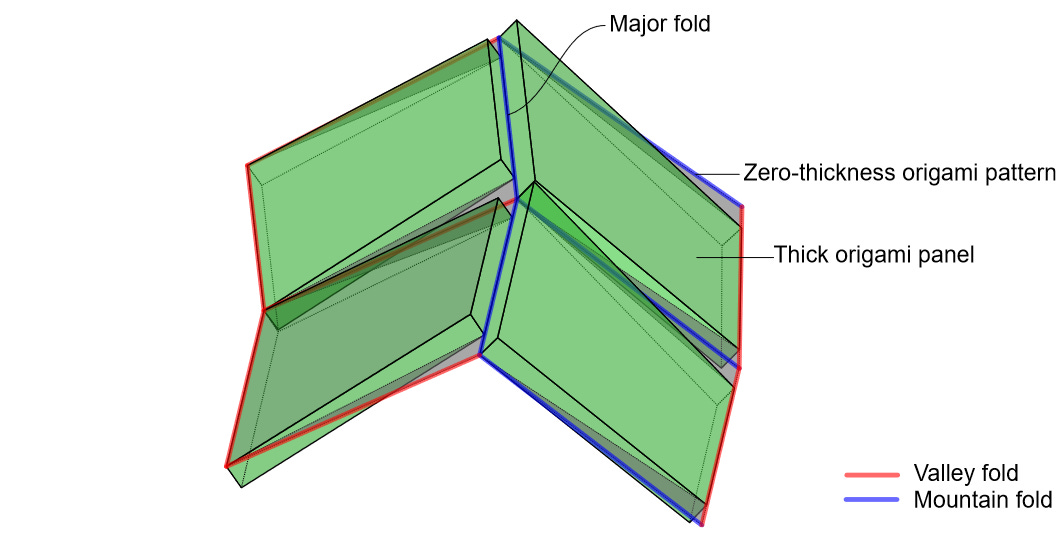
Traditional origami also assumes rigidity: the panels don’t shear or stretch during folding and the hinges are smooth and infinitely elastic. This is very often not the case when dealing with real-world materials. In fact, the wrapping pattern for Starshade is not rigid at all! The structure needs to stretch slightly around the hub while unfolding. If you upload the crease pattern to the Origami Simulator and turn on the strain feature, you can see this for yourself.
Origami engineers have to take this into account when picking materials and hinges to make sure none of these reach a failure point or deform plastically during deployment. In the case of Starshade, engineers wanted the structure to be stable in the fully folded and fully deployed configurations. The design process for the crease pattern actually minimizes the stretching of the edges between these two configurations (making these minimum energy states). This means the structure is unstable in intermediate stages of unfolding and will actually proceed to fully fold or fully unfold from intermediate stages.
These are only a few of the circumstances in which rules are broken (and we didn’t even get into kirigami: making cuts). In short, mathematical origami design is the backbone for designing deployable spacecraft, but it is in no way a blanket solution. Every project will have unique challenges and require creative solutions. That is all part of the fun!
Now that I’ve bored you with the technical parts of origami engineering, let me address a different question…
How did I end up here?
How exactly does a long-time hobby turn into a career option? It may not be as far-fetched as you think.
I never considered myself to be a space nut. Growing up, I was always labeled as the “artsy kid.” If a group project required drawing/painting/crafts, that was my job. I dabbled in many artistic hobbies — knitting, needle felt, computer animation, stop motion, you name it — but one of the most pervasive was origami. Mostly through YouTube, I learned how to fold complex models from crease patterns and the basics of design. I ordered huge sheets of origami paper, and spent hours on the floor making intricate creases. I got told off by teachers for folding in class. Despite all this, by the time I finished high school, my career plans lay in computational biology and bioinformatics. I wanted a STEM degree and I thought art would stay as a personal hobby.
My first quarter as a Caltech freshman, a friend suggested I attend a presentation by a JPL engineer entitled “Engineering Space Origami.” I watched in awe as Dr. Manan Arya explained the applications of origami in space and showcased the various projects he had worked on (including designing the fold patterns for Starshade). You can find a similar talk by Dr. Arya recorded here:
It took every ounce of courage I had to go up to him afterwards and ask if he was taking interns for the summer. Little did I know I had just met my to-be PhD advisor and kicked off a career in deployable structures. I got a mechanical engineering Bachelors — spending over a year as an intern with the JPL Advanced Deployable Structures Group, and another year with the Caltech Space Structures Lab. I’m now in the first year of my PhD with the Morphing Space Structures Lab at Stanford, advised by Dr. Arya.
A question I often get asked now is do I still fold origami in my free time? (What free time?) The answer is yes! I do! I understand the worry that turning a hobby into a career can make you hate it. For me personally though, deployable structures origami scratches a very different itch than the complex origami I make from paper. If anything, fighting to make a spacecraft design work makes me respect the simplicity and freedom of paper even more.
Is there a moral to this story?
I had support from amazing people (and a fair amount of luck on my side), but here are some of the key things I learned along the way:
There is plenty of space for art in science and engineering. Even if you don’t end up in a wacky field like space origami, I’ve noticed my artistic skills come in very useful for communication: Making powerpoints look pleasing and easy-to-follow, or preparing scientific figures for publication all require a keen eye for aesthetic and readability. Also, any engineering design work requires good visual-spatial skills and creative thinking!
Go to random seminars during undergrad. Even if the topic is only remotely interesting, or outside your field, you never know what you might learn, who you might meet, or what topic may plant a seed that will pop up a few years down the line. It’s fun to hear people talk about things there are passionate about, and there’s often free food too!
Reaching out (especially cold-emailing) is scary, but it can greatly pay off. I am shy, and I hate feeling like I’m bothering people. It took me a very long time to get comfortable selling myself and fighting for my own opportunities. But I never felt alone. Ask for advice, be it from peers, professors, colleagues, or role models. People love sharing their personal stories and I learned so much.
Thank you for letting me share the wonderous world of space origami! Free to reach out to me over email (haraszti@stanford.edu) if you have any questions or just want to talk origami! I’ll leave you with a series of cool origami-related videos.
Cool origami video dump
Even Veritasium did a video on space origami:
JPL’s PUFFER rover has an origami design:
Origami octopus limbs and wiggling worms (Renee Zhao, Stanford):
Origami tubes for bridges and spacecraft (Glaucio Paulino, Georgia Tech):
More Robert Lang:
Not origami, but ever wondered about exploring mathematics through knitting? Me neither:




Fantastic job Alexandra! I especially loved the visuals and careful walkthrough of the basics of origami - an art I have never learned about before. It's cool to see the mathematics behind it and how it is helping us explore the universe. Well done!